Electron. J. Diff. Equ., Vol. 2014 (2014), No. 265, pp. 1-10.

Relationship between solutions to a quasilinear elliptic equation in Orlicz spaces

Fei Fang, Zheng Zhou

Abstract:
In this article, we consider three types of solutions in Orlicz spaces for the quasilinear elliptic problem
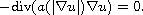
$$ -\hbox{div}(a(|\nabla u|)\nabla u)=0. $$
By applying a comparison principle, we establish the relationships between viscosity supersolutions, weak supersolutions, and superharmonic functions.

Submitted September 16, 2014. Published December 22, 2014.
Math Subject Classifications: 35J20, 35J65, 35J70, 35H30.
Key Words: Oilicz-Sobolev spaces; quasilinear elliptic equation; viscous solution.

Show me the PDF file (245 KB), TEX file, and other files for this article.

Fei Fang
School of Mathematical Sciences
Peking University
Beijing, 100871, China
email: fangfei68@163.com
Zheng Zhou
School of Applied Mathematical
Xiamen University of Technology
Xiamen 361024, China
email: zhouzhengslx@163.com

Return to the EJDE web page