Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 182, pp. 1-19.
Weakly locally thermal stabilization of Bresse systems
Nadine Najdi, Ali Wehbe
Abstract:
Fatori and Rivera [7] studied the stability of the Bresse system
with one distributed temperature dissipation law operating on the angle
displacement equation. They proved that, in general, the energy of the system
does not decay exponentially and they established the rate of
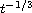 .
In this article, our goal is to extend their results, by taking into
consideration the important case when the thermal dissipation is locally
distributed and to improve the polynomial energy decay rate.
We then study the energy decay rate of Bresse system with one locally
thermal dissipation law. Under the equal speed wave propagation condition,
we establish an exponential energy decay rate. On the contrary,
we prove that the energy of the system decays, in general,
at the rate
.
In this article, our goal is to extend their results, by taking into
consideration the important case when the thermal dissipation is locally
distributed and to improve the polynomial energy decay rate.
We then study the energy decay rate of Bresse system with one locally
thermal dissipation law. Under the equal speed wave propagation condition,
we establish an exponential energy decay rate. On the contrary,
we prove that the energy of the system decays, in general,
at the rate
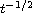 .
.
Submitted May 6, 2014. Published August 27, 2014.
Math Subject Classifications: 35B37, 35D05, 93C20, 73K50.
Key Words: Thermoelastic Bresse system; locally damping; strong stability;
exponential stability; polynomial stability;
frequency domain method; piece wise multiplier method.
Show me the PDF file (320 KB),
TEX file, and other files for this article.
 |
Nadine Najdi
Université de Valenciennes et du Hainaut Cambrésis
LAMAV, FR CNRS 2956
59313 Valenciennes Cedex 9, France
email: nadine.najdi@etu.univ-valenciennes.fr
|
|---|
 |
Ali Wehbe
Lebanese University,
Faculty of sciences I
EDST, Equipe EDP-AN
Hadath-Beirut, Lebanon
email: ali.wehbe@ul.edu.lb
|
|---|
Return to the EJDE web page
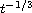 .
In this article, our goal is to extend their results, by taking into
consideration the important case when the thermal dissipation is locally
distributed and to improve the polynomial energy decay rate.
We then study the energy decay rate of Bresse system with one locally
thermal dissipation law. Under the equal speed wave propagation condition,
we establish an exponential energy decay rate. On the contrary,
we prove that the energy of the system decays, in general,
at the rate
.
In this article, our goal is to extend their results, by taking into
consideration the important case when the thermal dissipation is locally
distributed and to improve the polynomial energy decay rate.
We then study the energy decay rate of Bresse system with one locally
thermal dissipation law. Under the equal speed wave propagation condition,
we establish an exponential energy decay rate. On the contrary,
we prove that the energy of the system decays, in general,
at the rate
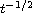 .
.

