Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 114, pp. 1-17.
Growth of solutions to higher-order linear differential equations
with entire coefficients
Habib Habib, Benharrat Belaidi
Abstract:
In this article, we discuss the order and
hyper-order of the linear differential equation
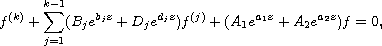
where
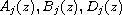 are entire functions
are entire functions
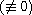 and
and
 are complex numbers
are complex numbers
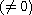 , and
, and
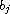 are real numbers.
Under certain conditions, we prove that every solution
are real numbers.
Under certain conditions, we prove that every solution
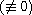 of the above equation is of infinite order. Then, we obtain an estimate
of the hyper-order. Finally, we give an estimate of the exponent of convergence
for distinct zeros of the functions
of the above equation is of infinite order. Then, we obtain an estimate
of the hyper-order. Finally, we give an estimate of the exponent of convergence
for distinct zeros of the functions
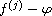
 ,
where
,
where
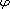 is an entire function
is an entire function
 and of order
and of order
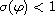 ,
while the solution f of the
differential equation is of infinite order. Our results extend the previous
results due to Chen, Peng and Chen and others.
,
while the solution f of the
differential equation is of infinite order. Our results extend the previous
results due to Chen, Peng and Chen and others.
Submitted November 22, 2013. Published April 21, 2014.
Math Subject Classifications: 34M10, 30D35.
Key Words: Linear differential equation; entire solution; order of growth;
hyper-order of growth; fixed point.
Show me the PDF file (312 KB),
TEX file, and other files for this article.
 |
Habib Habib
Department of Mathematics
Laboratory of Pure and Applied Mathematics
University of Mostaganem (UMAB)
B. P. 227 Mostaganem, Algeria
email: habibhabib2927@yahoo.fr
|
|---|
 |
Benharrat Belaïdi
Department of Mathematics
Laboratory of Pure and Applied Mathematics
University of Mostaganem (UMAB)
B. P. 227 Mostaganem, Algeria
email: belaidi@univ-mosta.dz
|
|---|
Return to the EJDE web page
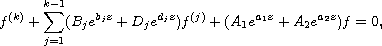
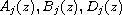 are entire functions
are entire functions
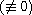 and
and
 are complex numbers
are complex numbers
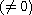 , and
, and
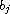 are real numbers.
Under certain conditions, we prove that every solution
are real numbers.
Under certain conditions, we prove that every solution
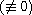 of the above equation is of infinite order. Then, we obtain an estimate
of the hyper-order. Finally, we give an estimate of the exponent of convergence
for distinct zeros of the functions
of the above equation is of infinite order. Then, we obtain an estimate
of the hyper-order. Finally, we give an estimate of the exponent of convergence
for distinct zeros of the functions
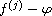
 ,
where
,
where
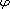 is an entire function
is an entire function
 and of order
and of order
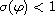 ,
while the solution f of the
differential equation is of infinite order. Our results extend the previous
results due to Chen, Peng and Chen and others.
,
while the solution f of the
differential equation is of infinite order. Our results extend the previous
results due to Chen, Peng and Chen and others.

