Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 10, pp. 1-10.
Solutions to Kirchhoff equations with combined nonlinearities
Ling Ding, Lin Li, Jing-Ling Zhang
Abstract:
We prove the existence of multiple positive solutions for the
Kirchhoff equation
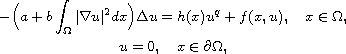
Here
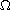 is an open bounded domain in
is an open bounded domain in
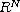 (
(
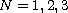 ),
),
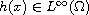 ,
,
 is a continuous function which
is asymptotically linear at zero and is asymptotically 3-linear at infinity.
Our main tools are the Ekeland's variational principle and the
mountain pass lemma.
is a continuous function which
is asymptotically linear at zero and is asymptotically 3-linear at infinity.
Our main tools are the Ekeland's variational principle and the
mountain pass lemma.
Submitted July 22, 2013. Published January 7, 2014.
Math Subject Classifications: 35J60, 35J40, 35B38.
Key Words: Kirchhoff equation; asymptotically linear; asymptotically 3-linear;
positive solution; mountain pass lemma.
Show me the PDF file (235 KB),
TEX file, and other files for this article.
 |
Ling Ding
School of Mathematics and Computer Science
Hubei University of Arts and Science
Hubei 441053, China
email: dingling1975@qq.com
|
|---|
 |
Lin Li
School of Mathematics and Statistics
Southwest University
Chongqing 400715, China
email:lilin420@gmail.com
|
|---|
 |
Jing-Ling Zhang
School of Mathematics and Computer Science
Hubei University of Arts and Science
Hubei 441053, China
email: 1293503066@qq.com
|
|---|
Return to the EJDE web page
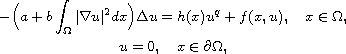
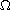 is an open bounded domain in
is an open bounded domain in
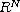 (
(
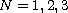 ),
),
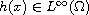 ,
,
 is a continuous function which
is asymptotically linear at zero and is asymptotically 3-linear at infinity.
Our main tools are the Ekeland's variational principle and the
mountain pass lemma.
is a continuous function which
is asymptotically linear at zero and is asymptotically 3-linear at infinity.
Our main tools are the Ekeland's variational principle and the
mountain pass lemma.


