Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 70, pp. 1-8.
Point rupture solutions of a singular elliptic equation
Huiqiang Jiang, Attou Miloua
Abstract:
We consider the elliptic equation
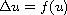
in a region
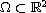 ,
where f is a positive continuous
function satisfying
,
where f is a positive continuous
function satisfying
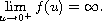
Motivated by the thin film equations, a solution
 is said to be a point
rupture solution if for some
is said to be a point
rupture solution if for some
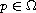 ,
,
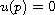 and
and
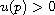 in
in
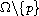 .
Our main
result is a sufficient condition on f for the existence of radial point
rupture solutions.
.
Our main
result is a sufficient condition on f for the existence of radial point
rupture solutions.
Submitted May 2, 2012. Published March 13, 2013.
Math Subject Classifications: 49Q20, 35J60, 35Q35.
Key Words: Thin film; point rupture; radial solution; singular equation.
Show me the PDF file (206 KB),
TEX file, and other files for this article.
 |
Huiqiang Jiang
Department of Mathematics, University of Pittsburgh
Pittsburgh, PA 15260, USA
email: hqjiang@pitt.edu
|
|---|
 |
Attou Miloua
Department of Mathematics, University of Pittsburgh
Pittsburgh, PA 15260, USA
email: atm33@pitt.edu
|
|---|
Return to the EJDE web page
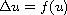
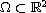 ,
where f is a positive continuous
function satisfying
,
where f is a positive continuous
function satisfying
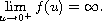
 is said to be a point
rupture solution if for some
is said to be a point
rupture solution if for some
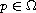 ,
,
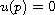 and
and
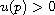 in
in
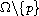 .
Our main
result is a sufficient condition on f for the existence of radial point
rupture solutions.
.
Our main
result is a sufficient condition on f for the existence of radial point
rupture solutions.

