This article is devoted to study the existence of solutions for the strongly nonlinear p(x)-elliptic problem
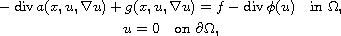
with
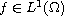 and
and
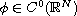 ,
also we will give some regularity results for these solutions.
,
also we will give some regularity results for these solutions.
Elhoussine Azroul, Hassane Hjiaj, Abdelfattah Touzani
Abstract:
This article is devoted to study the existence of solutions for
the strongly nonlinear p(x)-elliptic problem
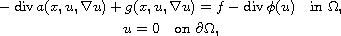
with
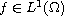 and
and
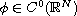 ,
also we will give some regularity results for these solutions.
,
also we will give some regularity results for these solutions.
Submitted May 22, 2012. Published March 8, 2013.
Math Subject Classifications: 35J20, 35J25, 35J60.
Key Words: Sobolev spaces with variable exponents; entropy solutions;
strongly nonlinear elliptic equations; boundary value problems.
Show me the PDF file (331 KB), TEX file, and other files for this article.
 |
Elhoussine Azroul University of Fez, Faculty of Sciences Dhar El Mahraz Laboratory LAMA, Department of Mathematics B.P. 1796 Atlas Fez, Morocco email: azroul_elhoussine@yahoo.fr |
|---|---|
 |
Hassane Hjiaj University of Fez, Faculty of Sciences Dhar El Mahraz Laboratory LAMA, Department of Mathematics B.P. 1796 Atlas Fez, Morocco email: hjiajhassane@yahoo.fr |
 |
Abdelfattah Touzani University of Fez, Faculty of Sciences Dhar El Mahraz Laboratory LAMA, Department of Mathematics B.P. 1796 Atlas Fez, Morocco email: atouzani07@gmail.com |
Return to the EJDE web page