Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 141, pp. 1-12.
Existence of solutions to fractional boundary-value
problems with a parameter
Ya-Ning Li, Hong-Rui Sun, Quan-Guo Zhang
Abstract:
This article concerns the existence of solutions to the fractional
boundary-value problem
![$$\displaylines{
-\frac{d}{dt} \big(\frac{1}{2} {}_0D_t^{-\beta}+
\frac{1}{2}{}_tD_{T}^{-\beta}\big)u'(t)=\lambda u(t)+\nabla F(t,u(t)),\quad
\hbox{a.e. } t\in[0,T], \cr
u(0)=0,\quad u(T)=0.
}$$](gifs/aa.gif)
First for the eigenvalue problem associated with it, we
prove that there is a sequence of positive and increasing real
eigenvalues; a characterization of the first eigenvalue is also
given. Then under different assumptions on the nonlinearity
F(t,u), we show the existence of weak solutions of the problem
when
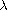 lies in various intervals. Our main tools are
variational methods and critical point theorems.
lies in various intervals. Our main tools are
variational methods and critical point theorems.
Submitted January 27, 2013. Published June 21, 2013.
Math Subject Classifications: 34A08, 34B09.
Key Words: Fractional differential equation; eigenvalue;
critical point theory; boundary value problem.
Show me the PDF file (257 KB),
TEX file, and other files for this article.
 |
Ya-Ning Li
School of Mathematics and Statistics
Lanzhou University
Lanzhou, Gansu 730000, China
email: liyn08@lzu.edu.cn
|
|---|
 |
Hong-Rui Sun
School of Mathematics and Statistics
Lanzhou University
Lanzhou, Gansu 730000, China
email: hrsun@lzu.edu.cn
|
|---|
 |
Quan-Guo Zhang
School of Mathematics and Statistics
Lanzhou University
Lanzhou, Gansu 730000, China
email: zhangqg07@lzu.edu.cn
|
|---|
Return to the EJDE web page
![$$\displaylines{
-\frac{d}{dt} \big(\frac{1}{2} {}_0D_t^{-\beta}+
\frac{1}{2}{}_tD_{T}^{-\beta}\big)u'(t)=\lambda u(t)+\nabla F(t,u(t)),\quad
\hbox{a.e. } t\in[0,T], \cr
u(0)=0,\quad u(T)=0.
}$$](gifs/aa.gif)
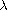 lies in various intervals. Our main tools are
variational methods and critical point theorems.
lies in various intervals. Our main tools are
variational methods and critical point theorems.


