Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 11, pp. 1-16.
Existence of infinitely many homoclinic orbits for second-order
systems involving Hamiltonian-type equations
Adel Daouas, Ammar Moulahi
Abstract:
We study the second-order differential system
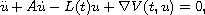
where A is an antisymmetric constant matrix and
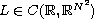 . We establish the existence
of infinitely many homoclinic solutions if W is of subquadratic
growth as
. We establish the existence
of infinitely many homoclinic solutions if W is of subquadratic
growth as
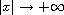 and L does not satisfy the global
positive definiteness assumption. In the particular case where A=0,
earlier results in the literature are generalized.
and L does not satisfy the global
positive definiteness assumption. In the particular case where A=0,
earlier results in the literature are generalized.
Submitted March 25, 2012. Published January 14, 2013.
Math Subject Classifications: 34C37, 37J45, 70H05.
Key Words: Homoclinic solutions; differential system; critical point.
Show me the PDF file (277 KB),
TEX file, and other files for this article.
 |
Adel Daouas
Mathematics department, College of sciences
Taibah University, Saudi Arabia
email: adaouas@taibahu.edu.sa
|
|---|
 |
Ammar Moulahi
College of Business and Economics
Qassim University, Saudi Arabia
email: ammar.moulahi@fsm.rnu.tn
|
|---|
Return to the EJDE web page
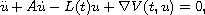
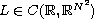 . We establish the existence
of infinitely many homoclinic solutions if W is of subquadratic
growth as
. We establish the existence
of infinitely many homoclinic solutions if W is of subquadratic
growth as
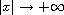 and L does not satisfy the global
positive definiteness assumption. In the particular case where A=0,
earlier results in the literature are generalized.
and L does not satisfy the global
positive definiteness assumption. In the particular case where A=0,
earlier results in the literature are generalized.

