Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 212, pp. 1-11.
Almost automorphic mild solutions of hyperbolic evolution equations
with stepanov-like almost automorphic forcing term
Indira Mishra, Dhirendra Bahuguna
Abstract:
This article concerns the existence and uniqueness of almost automorphic
solutions to the semilinear parabolic boundary differential equations
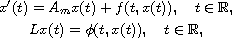
where
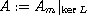 generates a hyperbolic analytic semigroup on a Banach
space
generates a hyperbolic analytic semigroup on a Banach
space
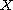 ,
with Stepanov-like almost automorphic nonlinear term, defined
on some extrapolated space
,
with Stepanov-like almost automorphic nonlinear term, defined
on some extrapolated space
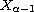 ,
for
,
for
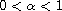 and
and
 takes values in the boundary space
takes values in the boundary space
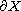 .
.
Submitted December 1, 2011. Published November 27, 2012.
Math Subject Classifications: 34K06, 34A12, 37L05.
Key Words: Almost automorphic; evolution equation; hyperbolic semigroups;
extrapolation spaces; interpolation spaces;
neutral differential equation; mild solution.
Show me the PDF file (251 KB),
TEX file, and other files for this article.
 |
Indira Mishra
Department of Mathematics & Statistics
Indian Institute of Technology-Kanpur
Kanpur - 208016, India
email: indiram@iitk.ac.in
|
|---|
 |
Dhirendra Bahuguna
Department of Mathematics & Statistics
Indian Institute of Technology-Kanpur
Kanpur - 208016, India
email: dhiren@iitk.ac.in
|
|---|
Return to the EJDE web page
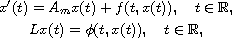
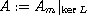 generates a hyperbolic analytic semigroup on a Banach
space
generates a hyperbolic analytic semigroup on a Banach
space
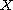 ,
with Stepanov-like almost automorphic nonlinear term, defined
on some extrapolated space
,
with Stepanov-like almost automorphic nonlinear term, defined
on some extrapolated space
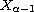 ,
for
,
for
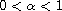 and
and
 takes values in the boundary space
takes values in the boundary space
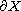 .
.

