In this article, we discuss the basic theory of boundary-value problems of fractional order
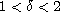 involving the Caputo derivative.
By applying the maximum principle, we obtain necessary conditions for
the existence of eigenfunctions, and show analytical lower and upper bounds
estimates of the eigenvalues. Also we obtain a sufficient condition
for the non existence of ordered solutions, by transforming
the problem into equivalent integro-differential equation.
By the method of lower and upper solution, we obtain a general
existence and uniqueness result: We generate two well defined monotone
sequences of lower and upper solutions which converge uniformly to the
actual solution of the problem.
While some fundamental results are obtained, we leave others as
open problems stated in a conjecture.
involving the Caputo derivative.
By applying the maximum principle, we obtain necessary conditions for
the existence of eigenfunctions, and show analytical lower and upper bounds
estimates of the eigenvalues. Also we obtain a sufficient condition
for the non existence of ordered solutions, by transforming
the problem into equivalent integro-differential equation.
By the method of lower and upper solution, we obtain a general
existence and uniqueness result: We generate two well defined monotone
sequences of lower and upper solutions which converge uniformly to the
actual solution of the problem.
While some fundamental results are obtained, we leave others as
open problems stated in a conjecture.
