Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 147, pp. 1-18.
Uniqueness and asymptotic behavior of boundary blow-up solutions
to semilinear elliptic problems with non-standard growth
Shuibo Huang, Wan-Tong Li, Qiaoyu Tian
Abstract:
In this article, we analyze uniqueness and asymptotic behavior
of boundary blow-up non-negative solutions to the semilinear elliptic equation
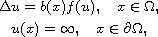
where
 is a bounded smooth domain,
b(x) is a non-negative function on
is a bounded smooth domain,
b(x) is a non-negative function on
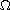 and f is non-negative on
and f is non-negative on
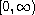 satisfying some structural conditions. The main novelty
of this paper is that uniqueness is established only by imposing
a control on their growth on the weights b(x) near
satisfying some structural conditions. The main novelty
of this paper is that uniqueness is established only by imposing
a control on their growth on the weights b(x) near
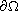 and the nonlinear term f at infinite, rather than requiring them to
have a precise asymptotic behavior. Our proof is based on the
method of sub and super-solutions and the Safonov iteration technique.
and the nonlinear term f at infinite, rather than requiring them to
have a precise asymptotic behavior. Our proof is based on the
method of sub and super-solutions and the Safonov iteration technique.
Submitted July 20, 2012. Published August 21, 2012.
Math Subject Classifications: 35J65, 35J60, 74G30, 35B40.
Key Words: Boundary blow-up solutions; uniqueness; asymptotic behavior.
Show me the PDF file (306 KB),
TEX file, and other files for this article.
 |
Shuibo Huang
School of Mathematics and Statistics
Lanzhou University
Lanzhou, Gansu 730000, China
email: huangshuibo2008@163.com
|
|---|
 |
Wan-Tong Li
School of Mathematics and Statistics
Lanzhou University
Lanzhou, Gansu 730000, China
email: wtli@lzu.edu.cn
|
|---|
 |
Qiaoyu Tian
Department of Mathematics
Gansu Normal University for Nationalities
Hezuo, Gansu 747000, China
email: tianqiaoyu2004@163.com
|
|---|
Return to the EJDE web page
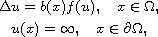
 is a bounded smooth domain,
b(x) is a non-negative function on
is a bounded smooth domain,
b(x) is a non-negative function on
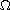 and f is non-negative on
and f is non-negative on
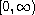 satisfying some structural conditions. The main novelty
of this paper is that uniqueness is established only by imposing
a control on their growth on the weights b(x) near
satisfying some structural conditions. The main novelty
of this paper is that uniqueness is established only by imposing
a control on their growth on the weights b(x) near
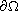 and the nonlinear term f at infinite, rather than requiring them to
have a precise asymptotic behavior. Our proof is based on the
method of sub and super-solutions and the Safonov iteration technique.
and the nonlinear term f at infinite, rather than requiring them to
have a precise asymptotic behavior. Our proof is based on the
method of sub and super-solutions and the Safonov iteration technique.


