Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 04, pp. 1-10.
Monotone iterative method and regular singular
nonlinear BVP in the presence of reverse ordered upper
and lower solutions
Amit K. Verma
Abstract:
Monotone iterative technique is employed for studying the existence
of solutions to the second-order nonlinear singular boundary
value problem
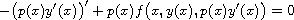
for
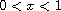 and
and
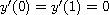 .
Here
.
Here
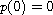 and
and
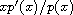 is analytic at
is analytic at
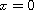 .
The source function
.
The source function
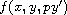 is Lipschitz in
is Lipschitz in
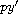 and one sided Lipschitz in
and one sided Lipschitz in
 .
The initial approximations are upper solution
.
The initial approximations are upper solution
 and lower
solution
and lower
solution
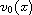 which can be ordered in one way
which can be ordered in one way
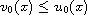 or the other
or the other
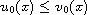 .
.
Submitted October 19, 2011. Published January 9, 2012.
Math Subject Classifications: 34B16.
Key Words: Monotone iterative technique; lower and upper solutions;
Neumann boundary conditions.
Show me the PDF file (226 KB),
TEX file, and other files for this article.
 |
Amit K. Verma
Department of Mathematics, BITS Pilani
Pilani - 333031, Rajasthan, India
Phone +919413789285; fax: +911596244183
email: amitkverma02@yahoo.co.in, akverma@bits-pilani.ac.in
|
|---|
Return to the EJDE web page
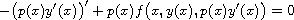
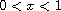 and
and
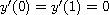 .
Here
.
Here
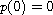 and
and
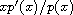 is analytic at
is analytic at
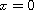 .
The source function
.
The source function
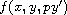 is Lipschitz in
is Lipschitz in
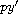 and one sided Lipschitz in
and one sided Lipschitz in
 .
The initial approximations are upper solution
.
The initial approximations are upper solution
 and lower
solution
and lower
solution
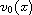 which can be ordered in one way
which can be ordered in one way
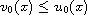 or the other
or the other
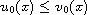 .
.
