Electron. J. Diff. Equ., Vol. 2011 (2011), No. 83, pp. 1-10.

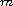Positive solutions for a nonlinear n-th order m-point boundary-value problem

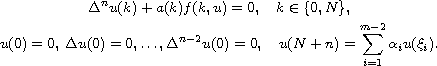
Jiehua Zhang, Yanping Guo, Yude Ji

Abstract:
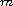Using the Leggett-Williams fixed point theorem in cones, we prove the existence of at least three positive solutions to the nonlinear $n$-th order $m$-point boundary-value problem
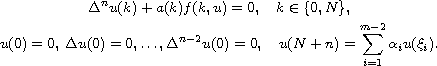
$$\displaylines{ \Delta^{n}u(k)+a(k)f(k,u)=0, \quad k\in \{0,N\},\cr u(0)=0,\; \Delta u(0)=0, \dots, \Delta^{n-2}u(0)=0,\quad u(N+n)=\sum_{i=1}^{m-2}\alpha_iu(\xi_i). }$$

Submitted March 12, 2010. Published June 24, 2011.
Math Subject Classifications: 39A10.
Key Words: Boundary value problem; positive solution; fixed point theorem; Green's function.

Show me the PDF file (225 KB), TEX file, and other files for this article.

Jiehua Zhang
College of Sunshine, Fuzhou University
Fuzhou 350015, China
email: jiehuahappy@163.com
Yanping Guo
College of Sciences
Hebei University of Science and Technology
Shijiazhuang 050018, China
email: guoyanping65@sohu.com
Yude Ji
College of Sciences
Hebei University of Science and Technology
Shijiazhuang 050018, China
email: jiyude-1980@163.com

Return to the EJDE web page