Using the coincidence degree theory by Mawhin, we prove the existence of periodic solutions for the second-order delay differential equations with impulses
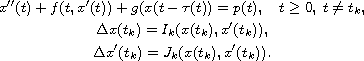
We obtain new existence results and illustrated them by an example.
Lijun Pan
Abstract:
Using the coincidence degree theory by Mawhin,
we prove the existence of periodic solutions for the
second-order delay differential equations with impulses
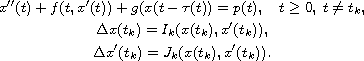
We obtain new existence results and illustrated them by an example.
Submitted January 28, 2011. Published March 3, 2011.
Math Subject Classifications: 34K13, 34K45.
Key Words: Second-order delay differential equations; impulses;
periodic solution; coincidence degree.
Show me the PDF file (224 KB), TEX file, and other files for this article.
 |
Lijun Pan School of Mathematics, Jia Ying University Meizhou Guangdong, 514015, China email: plj1977@126.com |
|---|
Return to the EJDE web page