Using a variational approach, we prove the existence of solutions for the degenerate quasilinear elliptic system
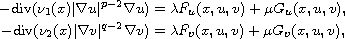
with Dirichlet boundary conditions.
Ghasem Alizadeh Afrouzi, Somayeh Mahdavi, Nikolaos B. Zographopoulos
Abstract:
Using a variational approach, we prove the existence of
solutions for the degenerate quasilinear elliptic system
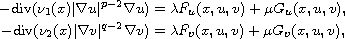
with Dirichlet boundary conditions.
Submitted November 12, 2011. Published December 14, 2011.
Math Subject Classifications: 34B18, 35B40, 35J65.
Key Words: Non-uniformly elliptic system; mountain pass theorem;
minimum principle.
Show me the PDF file (221 KB), TEX file, and other files for this article.
 |
Ghasem Alizadeh Afrouzi Department of Mathematics, Faculty of Mathematical Sciences University of Mazandaran, Babolsar, Iran email: afrouzi@umz.ac.ir |
|---|---|
 |
Somayeh Mahdavi Department of Mathematics, Faculty of Mathematical Sciences University of Mazandaran, Babolsar, Iran email: smahdavi@umz.ac.ir |
| Nikolaos B. Zographopoulos University of Military Education, Hellenic Army Academy Department of Mathematics & Engineering Sciences Vari - 16673, Athens, Greece email: nzograp@gmail.com, zographopoulosn@sse.gr |
Return to the EJDE web page