Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 145, pp. 1-11.
Asymptotically linear fourth-order elliptic problems
whose nonlinearity crosses several eigenvalues
Evandro Monteiro
Abstract:
In this article we prove the existence of multiple solutions for
the fourth-order elliptic problem
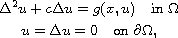
where
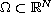 is a bounded domain,
is a bounded domain,
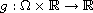 is a function
of class
is a function
of class
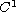 such that
such that
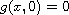 and it
is asymptotically linear at infinity.
We study the cases when the parameter c is less than the
first eigenvalue, and between two consecutive eigenvalues
of the Laplacian. To obtain solutions we use the Saddle Point Theorem,
the Linking Theorem, and Critical Groups Theory.
and it
is asymptotically linear at infinity.
We study the cases when the parameter c is less than the
first eigenvalue, and between two consecutive eigenvalues
of the Laplacian. To obtain solutions we use the Saddle Point Theorem,
the Linking Theorem, and Critical Groups Theory.
Submitted February 15, 2011. Published November 2, 2011.
Math Subject Classifications: 35J30, 35J35.
Key Words: Asymptotically linear; Morse theory; shifting theorem;
multiplicity of solutions.
Show me the PDF file (231 KB),
TEX file, and other files for this article.
 |
Evandro Monteiro
UNIFAL-MG, Rua Gabriel Monteiro da Silva, 700. Centro
CEP 37130-000 Alfenas-MG, Brazil
email: evandromonteiro@unifal-mg.edu.br
|
|---|
Return to the EJDE web page
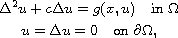
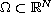 is a bounded domain,
is a bounded domain,
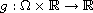 is a function
of class
is a function
of class
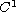 such that
such that
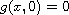 and it
is asymptotically linear at infinity.
We study the cases when the parameter c is less than the
first eigenvalue, and between two consecutive eigenvalues
of the Laplacian. To obtain solutions we use the Saddle Point Theorem,
the Linking Theorem, and Critical Groups Theory.
and it
is asymptotically linear at infinity.
We study the cases when the parameter c is less than the
first eigenvalue, and between two consecutive eigenvalues
of the Laplacian. To obtain solutions we use the Saddle Point Theorem,
the Linking Theorem, and Critical Groups Theory.
