Electron. J. Diff. Equ.,
Vol. 2011(2011), No. 03, pp. 1-26.
Solvability of degenerated parabolic equations without sign
condition and three unbounded nonlinearities
Youssef Akdim, Jaouad Bennouna, Mounir Mekkour
Abstract:
In this article, we study the problem
![$$\displaylines{
\frac{\partial}{\partial t} b(x, u)-\hbox{div}(a(x,t,u,D u))
+H(x,t,u,Du) = f\quad \hbox{in } \Omega\times ]0,T[,\cr
b(x,u)(t=0)=b(x,u_0)\quad\hbox{in } \Omega,\cr
u=0\quad\hbox{in } \partial\Omega\times ]0,T[
}$$](gifs/aa.gif)
in the framework of weighted Sobolev spaces, with
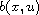 unbounded function on u. The main contribution of our work is to
prove the existence of a renormalized solution without the sign
condition and the coercivity condition on
unbounded function on u. The main contribution of our work is to
prove the existence of a renormalized solution without the sign
condition and the coercivity condition on
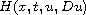 . The
critical growth condition on
. The
critical growth condition on
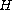 is with respect to
Du and no growth condition with respect to u.
The second term f belongs to
is with respect to
Du and no growth condition with respect to u.
The second term f belongs to
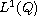 , and
, and
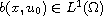 .
.
Submitted June 28, 2010. Published January 4, 2011.
Math Subject Classifications: A7A15, A6A32, 47D20.
Key Words: Weighted Sobolev spaces; truncations;
time-regularization; renormalized solutions.
Show me the PDF file (341 KB),
TEX file, and other files for this article.
 |
Youssef Akdim
Département de Mathématiques
Faculté des Sciences Dhar-Mahraz, Fès, Morocco
email: akdimyoussef@yahoo.fr |
|---|
 |
Jaouad Bennouna
Département de Mathématiques
Faculté des Sciences Dhar-Mahraz, Fès, Morocco
email: jbennouna@hotmail.com |
|---|
 |
Mounir Mekkour
Département de Mathématiques
Faculté des Sciences Dhar-Mahraz, Fès, Morocco
email: mekkour.mounir@yahoo.fr |
|---|
Return to the EJDE web page
![$$\displaylines{
\frac{\partial}{\partial t} b(x, u)-\hbox{div}(a(x,t,u,D u))
+H(x,t,u,Du) = f\quad \hbox{in } \Omega\times ]0,T[,\cr
b(x,u)(t=0)=b(x,u_0)\quad\hbox{in } \Omega,\cr
u=0\quad\hbox{in } \partial\Omega\times ]0,T[
}$$](gifs/aa.gif)
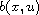 unbounded function on u. The main contribution of our work is to
prove the existence of a renormalized solution without the sign
condition and the coercivity condition on
unbounded function on u. The main contribution of our work is to
prove the existence of a renormalized solution without the sign
condition and the coercivity condition on
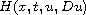 . The
critical growth condition on
. The
critical growth condition on
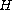 is with respect to
Du and no growth condition with respect to u.
The second term f belongs to
is with respect to
Du and no growth condition with respect to u.
The second term f belongs to
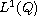 , and
, and
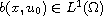 .
.


