In this note we consider the regularity of solutions to 3-D nematic liquid crystal flows, we prove that if either
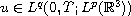 ,
,
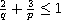 ,
,
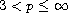 ;
or
;
or
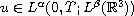 ,
,
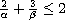 ,
,
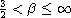 , then the solution
, then the solution
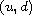 is regular on
is regular on
![$(0,T]$](gifs/ah.gif) .
.
Qiao Liu, Shangbin Cui
Abstract:
In this note we consider the regularity of solutions to 3-D
nematic liquid crystal flows, we prove that if either
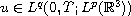 ,
,
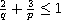 ,
,
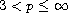 ;
or
;
or
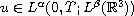 ,
,
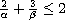 ,
,
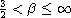 , then the solution
, then the solution
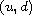 is regular on
is regular on
![$(0,T]$](gifs/ah.gif) .
.
Submitted November 4, 2010. Published December 6, 2010.
Math Subject Classifications: 76A15, 35B65, 35Q35.
Key Words: Liquid crystal flow; initial value problem;
regularity of solutions.
Show me the PDF file (191 KB), TEX file, and other files for this article.
 |
Qiao Liu Department of Mathematics, Sun Yat-sen University Guangzhou, Guangdong 510275, China email: liuqao2005@lzu.cn, liuqao2005@163.com |
|---|---|
| Shangbin Cui Department of Mathematics, Sun Yat-sen University Guangzhou, Guangdong 510275, China email: cuisb3@yahoo.com.cn |
Return to the EJDE web page