We consider the global well-posedness problem of a one-parameter family of coupled KdV-type systems both in the periodic and non-periodic setting. When the coupling parameter
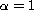 ,
we prove the global
well-posedness in
,
we prove the global
well-posedness in
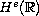 for
for
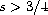 and
and
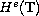 for
for
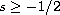 via the I-method developed
by Colliander-Keel-Staffilani-Takaoka-Tao [5].
When
via the I-method developed
by Colliander-Keel-Staffilani-Takaoka-Tao [5].
When
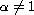 ,
as in the local theory [14],
certain resonances occur, closely depending on the value of
,
as in the local theory [14],
certain resonances occur, closely depending on the value of
 .
We use the Diophantine conditions to characterize the resonances.
Then, via the second iteration of the I-method, we establish a
global well-posedness result in
.
We use the Diophantine conditions to characterize the resonances.
Then, via the second iteration of the I-method, we establish a
global well-posedness result in
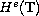 ,
,
 ,
where
,
where
![$\widetilde{s}= \widetilde{s}(\alpha) \in (5/7, 1]$](gifs/ai.gif) is determined by the
Diophantine characterization of certain constants derived from the
coupling parameter
is determined by the
Diophantine characterization of certain constants derived from the
coupling parameter
 .
We also show that the third iteration of
the I-method fails in this case.
.
We also show that the third iteration of
the I-method fails in this case.
