In this article we study the fractional semilinear mixed Volterra-Fredholm integrodifferential equation

where
![$t\in [t_0,T]$](gifs/ab.gif) ,
,
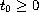 ,
,
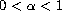 , and
, and
 is a given function. We prove the existence and uniqueness
of solutions to this equation, with a nonlocal condition.
is a given function. We prove the existence and uniqueness
of solutions to this equation, with a nonlocal condition.
Mohammed M. Matar
Abstract:
In this article we study the fractional semilinear mixed
Volterra-Fredholm integrodifferential equation

where
![$t\in [t_0,T]$](gifs/ab.gif) ,
,
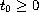 ,
,
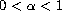 , and
, and
 is a given function. We prove the existence and uniqueness
of solutions to this equation, with a nonlocal condition.
is a given function. We prove the existence and uniqueness
of solutions to this equation, with a nonlocal condition.
Submitted September 12, 2009. Published December 1, 2009.
Math Subject Classifications: 45J05, 26A33, 34A12.
Key Words: Fractional integrodifferential equations;
mild solution; nonlocal condition; Banach fixed point.
Show me the PDF file (193 KB), TEX file, and other files for this article.
 |
Mohammed M. Matar Department of Mathematics, Al-Azhar University of Gaza P. O. Box 1277, Gaza, Palestine email: mohammed_mattar@hotmail.com |
|---|
Return to the EJDE web page