Electron. J. Diff. Equ.,
Vol. 2009(2009), No. 108, pp. 1-6.
Positive solutions for semi-linear elliptic
equations in exterior domains
Habib Maagli, Sameh Turki, Noureddine Zeddini
Abstract:
We prove the existence of a solution, decaying to zero at
infinity, for the second order differential
equation
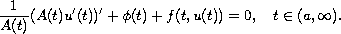
Then we give a simple proof, under some sufficient conditions which
unify and generalize most of those given in the bibliography, for
the existence of a positive solution for the semilinear second order
elliptic equation
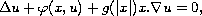
in an exterior domain of the Euclidean space
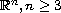 .
.
Submitted August 12, 2009. Published September 10, 2009.
Math Subject Classifications: 34A12, 35J60.
Key Words: Positive solutions; nonlinear elliptic equations; exterior domain.
Show me the PDF file (198 KB),
TEX file, and other files for this article.
 |
Habib Maagli
Département de Mathématiques, Faculté des Sciences de Tunis
Campus Universitaire, 2092 Tunis, Tunisia
email: habib.maagli@fst.rnu.tn
|
|---|
 |
Sameh Turki
Département de Mathématiques, Faculté des Sciences de Tunis
Campus Universitaire, 2092 Tunis, Tunisia
email: sameh.turki@ipein.rnu.tn
|
|---|
 |
Noureddine Zeddini
Département de Mathématiques, Faculté des Sciences de Tunis
Campus Universitaire, 2092 Tunis, Tunisia
email: noureddine.zeddini@ipein.rnu.tn
|
|---|
Return to the EJDE web page
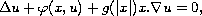
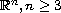 .
.


