Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 61, pp. 1-12.
Three solutions for singular p-Laplacian type equations
Zhou Yang, Di Geng, Huiwen Yan
Abstract:
In this paper, we consider the singular
 -Laplacian type equation
-Laplacian type equation
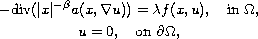
where
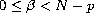 ,
,
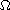 is a smooth bounded domain in
is a smooth bounded domain in
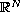 containing the origin,
containing the origin,
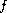 satisfies some growth
and singularity conditions. Under some mild assumptions on
satisfies some growth
and singularity conditions. Under some mild assumptions on
 ,
applying the three critical points theorem developed
by Bonanno, we establish the existence of at least three distinct
weak solutions to the above problem if
,
applying the three critical points theorem developed
by Bonanno, we establish the existence of at least three distinct
weak solutions to the above problem if
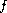 admits some
hypotheses on the behavior at
admits some
hypotheses on the behavior at
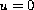 or perturbation property.
or perturbation property.
Submitted January 14, 2008. Published April 22, 2008.
Math Subject Classifications: 35J60.
Key Words: p-Laplacian operator; singularity; multiple solutions.
Show me the
PDF file (264 KB),
TEX file, and other files for this article.
 |
Zhou Yang
School of Math. Sci., South China Normal University
Guangzhou 510631, China
email: yangzhou@scnu.edu.cn |
|---|
 |
Di Geng
School of Math. Sci., South China Normal University
Guangzhou 510631, China
email: gengdi@scnu.edu.cn |
|---|
 |
Huiwen Yan
School of Math. Sci., South China Normal University
Guangzhou 510631, China
email: hwyan10@yahoo.com.cn |
|---|
Return to the EJDE web page
 -Laplacian type equation
-Laplacian type equation
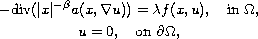
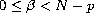 ,
,
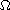 is a smooth bounded domain in
is a smooth bounded domain in
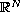 containing the origin,
containing the origin,
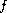 satisfies some growth
and singularity conditions. Under some mild assumptions on
satisfies some growth
and singularity conditions. Under some mild assumptions on
 ,
applying the three critical points theorem developed
by Bonanno, we establish the existence of at least three distinct
weak solutions to the above problem if
,
applying the three critical points theorem developed
by Bonanno, we establish the existence of at least three distinct
weak solutions to the above problem if
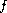 admits some
hypotheses on the behavior at
admits some
hypotheses on the behavior at
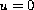 or perturbation property.
or perturbation property.


