In this paper, we study the existence of solutions for the nonlinear elliptic system
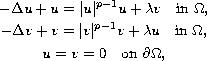
where
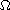 is a exterior domain in
is a exterior domain in
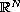 ,
,
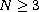 .
We show that the system possesses at least one nontrivial positive solution.
.
We show that the system possesses at least one nontrivial positive solution.
Huijuan Gu, Jianfu Yang, Xiaohui Yu
Abstract:
In this paper, we study the existence
of solutions for the nonlinear elliptic system
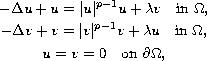
where
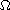 is a exterior domain in
is a exterior domain in
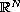 ,
,
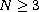 .
We show that the system possesses at least one nontrivial positive solution.
.
We show that the system possesses at least one nontrivial positive solution.
Submitted June 28, 2008. Published August 28, 2008.
Math Subject Classifications: 35J50, 35B32.
Key Words: Exterior domain; nonlinear elliptic system; existence result.
Show me the PDF file (252 KB), TEX file, and other files for this article.
| Huijuan Gu Department of Mathematics, Jiangxi Normal University Nanchang, Jiangxi 330022, China email: ruobing411@yahoo.com.cn |
| Jianfu Yang Department of Mathematics, Jiangxi Normal University Nanchang, Jiangxi 330022, China email: jfyang_2000@yahoo.com |
| Xiaohui Yu China Institute for Advanced Study Central University of Finance and Economics Beijing 100081, China email: yuxiao_211@163.com |
Return to the EJDE web page