Yun Chen, Baoqiang Yan, Lili Zhang
Abstract:
Using a fixed point theorem in cones, this paper shows
the existence of positive solutions for the singular
three-point boundary-value problem
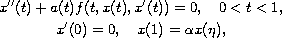
where
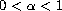 ,
,
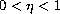 , and
, and
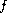 may change sign and may
be singular at
may change sign and may
be singular at
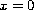 and
and
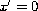 .
.
Submitted September 15, 2006. Published April 25, 2007.
Math Subject Classifications: 34B15, 34B10.
Key Words: Three-point boundary value problem; singularity;
positive solutions; fixed point theorem.
Show me the PDF file (206K), TEX file, and other files for this article.
 |
Yun Chen Department of Mathematics Shandong Normal University Jinan, 250014, China email: chenyun001982@126.com |
|---|---|
 |
Baoqiang Yan Department of Mathematics Shandong Normal University Jinan, 250014, China email: yanbqcn@yahoo.com.cn |
 |
Lili Zhang Department of Mathematics Shandong Normal University Jinan, 250014, China email: kuaile100@163.com |
Return to the EJDE web page