Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 177, pp. 1-9.
Existence of positive solutions for p(x)-Laplacian problems
Ghasem A. Afrouzi, Horieh Ghorbani
Abstract:
We consider the system of differential equations
![$$\displaylines{
-\Delta_{p(x)} u=\lambda [g(x)a(u) + f(v)] \quad\hbox{in }\Omega\cr
-\Delta_{q(x)} v=\lambda [g(x)b(v) + h(u)] \quad\hbox{in }\Omega\cr
u=v= 0 \quad\hbox{on } \partial \Omega
}$$](gifs/aa.gif)
where
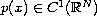 is a radial symmetric function
such that
is a radial symmetric function
such that
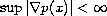 ,
,
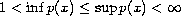 ,
and where
,
and where
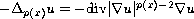 which is called the
which is called the
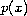 -Laplacian.
We discuss the existence of positive solution via
sub-super-solutions without assuming sign conditions on
-Laplacian.
We discuss the existence of positive solution via
sub-super-solutions without assuming sign conditions on
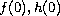 .
.
Submitted July 18, 2007. Published December 17, 2007.
Math Subject Classifications: 35J60, 35B30, 35B40
Key Words: Positive radial solutions; p(x)-Laplacian problems;
boundary value problems.
Show me the
PDF file (221 KB),
TEX file, and other files for this article.
 |
Ghasem A. Afrouzi
Department of Mathematics
Faculty of Basic Sciences
Mazandaran University, Babolsar, Iran
email: afrouzi@umz.ac.ir
|
|---|
 |
Horieh Ghorbani
Department of Mathematics
Faculty of Basic Sciences
Mazandaran University, Babolsar, Iran
email: seyed86@yahoo.com
|
|---|
Return to the EJDE web page
![$$\displaylines{
-\Delta_{p(x)} u=\lambda [g(x)a(u) + f(v)] \quad\hbox{in }\Omega\cr
-\Delta_{q(x)} v=\lambda [g(x)b(v) + h(u)] \quad\hbox{in }\Omega\cr
u=v= 0 \quad\hbox{on } \partial \Omega
}$$](gifs/aa.gif)
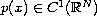 is a radial symmetric function
such that
is a radial symmetric function
such that
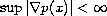 ,
,
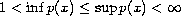 ,
and where
,
and where
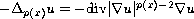 which is called the
which is called the
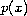 -Laplacian.
We discuss the existence of positive solution via
sub-super-solutions without assuming sign conditions on
-Laplacian.
We discuss the existence of positive solution via
sub-super-solutions without assuming sign conditions on
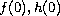 .
.

