Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 121, pp. 1-10.
A minimax inequality for a class of functionals and
applications to the existence of solutions for
two-point boundary-value problems
Ghasem Alizadeh Afrouzi, Shapour Heidarkhani
Abstract:
In this paper, we establish an equivalent statement to minimax
inequality for a special class of functionals. As an application,
we prove the existence of three solutions to the Dirichlet
problem

where
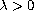 ,
,
![$f:[a,b]\times \mathbb{R}\to \mathbb{R}$](gifs/ac.gif) is a
continuous function which changes sign on
is a
continuous function which changes sign on
![$[a,b]\times \mathbb{R}$](gifs/ad.gif) and
and
![$m(x)\in C([a,b])$](gifs/ae.gif) is a positive function.
is a positive function.
Submitted August 22, 2006. Published October 2, 2006.
Math Subject Classifications: 35J65.
Key Words: Minimax inequality; critical point; three solutions;
multiplicity results; Dirichlet problem.
Show me the
PDF file (220K),
TEX file, and other files for this article.
 |
Ghasem Alizadeh Afrouzi
Department of Mathematics
Faculty of Basic Sciences
Mazandaran University, Babolsar, Iran
email: afrouzi@umz.ac.ir |
|---|
 |
Shapour Heidarkhani
Department of Mathematics
Faculty of Basic Sciences
Mazandaran University, Babolsar, Iran
email: s.heidarkhani@umz.ac.ir
|
|---|
Return to the EJDE web page

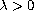 ,
,
![$f:[a,b]\times \mathbb{R}\to \mathbb{R}$](gifs/ac.gif) is a
continuous function which changes sign on
is a
continuous function which changes sign on
![$[a,b]\times \mathbb{R}$](gifs/ad.gif) and
and
![$m(x)\in C([a,b])$](gifs/ae.gif) is a positive function.
is a positive function.

