Let
 be a time scale with
be a time scale with
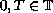 .
We investigate the existence and multiplicity of positive solutions
to the nonlinear second-order three-point boundary-value problem
.
We investigate the existence and multiplicity of positive solutions
to the nonlinear second-order three-point boundary-value problem
![$$\displaylines{
u^{\Delta\nabla}(t)+a(t)f(u(t))=0,\quad t\in[0, T]\subset \mathbb{T},\cr
u(0)=\beta u(\eta),\quad u(T)=\alpha u(\eta)
}$$](gifs/ac.gif)
on time scales
 , where
, where
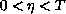 ,
,
 ,
,
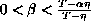 are given constants.
are given constants.
Hua Luo, Qiaozhen Ma
Abstract:
Let
 be a time scale with
be a time scale with
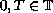 .
We investigate the existence and multiplicity of positive solutions
to the nonlinear second-order three-point boundary-value problem
.
We investigate the existence and multiplicity of positive solutions
to the nonlinear second-order three-point boundary-value problem
![$$\displaylines{
u^{\Delta\nabla}(t)+a(t)f(u(t))=0,\quad t\in[0, T]\subset \mathbb{T},\cr
u(0)=\beta u(\eta),\quad u(T)=\alpha u(\eta)
}$$](gifs/ac.gif)
on time scales
 , where
, where
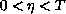 ,
,
 ,
,
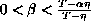 are given constants.
are given constants.
Submitted September 1, 2004. Published February 1, 2005.
Math Subject Classifications: 34B18, 39A10.
Key Words: Time scales; three-point boundary value problems; cone;
fixed points; positive solutions.
Show me the PDF file (248K), TEX file, and other files for this article.
 |
Hua Luo College of Mathematics and Information Science Northwest Normal University Lanzhou 730070, Gansu, China email: luohua@nwnu.edu.cn |
|---|---|
 |
Qiaozhen Ma College of Mathematics and Information Science Northwest Normal University Lanzhou 730070, Gansu, China email: maqzh@nwnu.edu.cn |
Return to the EJDE web page