This article presents a new approach for investigating the oscillation properties of second order linear differential equations with a damped term containing a deviating argument
![$$
x''(t)-[P(t)x(r(t))]'+Q(t)x(l(t))=0,\quad r(t)\leq t.
$$](gifs/aa.gif)
To study this equation, a specially adapted version of Sturmian Comparison Method is developed and the following results are obtained:
(a) A comprehensive description of all critical (threshold) states with respect to its oscillation properties for a linear autonomous delay differential equation

(b) Two versions of Sturm-Like Comparison Theorems. Based on these Theorems, sharp conditions under which all solutions are oscillatory for specific realizations of
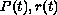 and
and
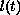 are obtained.
These conditions are formulated as the unimprovable analogues of the classical
Knezer Theorem which is well-known for ordinary differential equations
(
are obtained.
These conditions are formulated as the unimprovable analogues of the classical
Knezer Theorem which is well-known for ordinary differential equations
(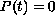 ,
,
 ).
).
(c) Upper bounds for intervals, where any solution has at least one zero.

