On the sixth line of Theorem 2.1, the expression
![$A^\epsilon\in L^\infty([0,T];H^s(\mathbb{R}^N))$](gifs/ab.gif) should be replaced by
should be replaced by
![$|A^\epsilon|-\sqrt{\mathcal{C}}\in
L^\infty([0,T];H^s(\mathbb{R}^N))$](gifs/ac.gif) .
.
On the fourteenth line of Theorem 2.2, the expression
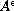 should be replaced by
should be replaced by
![$|A^\epsilon|-\sqrt{\mathcal{C}}\in L^\infty([0,T];H^s(\mathbb{R}^N))$](gifs/ae.gif) .
.
See last page of this manuscript for details.
Hailiang Li & Chi-Kun Lin
Abstract:
This paper concerns the well-posedness and semiclassical limit of
nonlinear Schrodinger-Poisson systems. We show the local
well-posedness and the existence of semiclassical limit of the
two models for initial data with Sobolev regularity, before shocks
appear in the limit system. We establish the existence of a global
solution and show the time-asymptotic behavior of a classical
solutions of Schrodinger-Poisson system for a fixed re-scaled
Planck constant.
Submitted April 1, 2002. Published September 8, 2003.
Math Subject Classifications: 35A05, 35Q55.
Key Words: Schrodinger-Poisson system, quantum hydrodynamics,
Euler-Poisson system, semiclassical limit, WKB expansion,
quasilinear symmetric hyperbolic system.
An addendum was attached on August 17, 2006.
The authors made the following two corrections:
On the sixth line of Theorem 2.1, the expression
![$A^\epsilon\in L^\infty([0,T];H^s(\mathbb{R}^N))$](gifs/ab.gif) should be replaced by
should be replaced by
![$|A^\epsilon|-\sqrt{\mathcal{C}}\in
L^\infty([0,T];H^s(\mathbb{R}^N))$](gifs/ac.gif) .
.
On the fourteenth line of Theorem 2.2, the expression
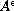 should be replaced by
should be replaced by
![$|A^\epsilon|-\sqrt{\mathcal{C}}\in L^\infty([0,T];H^s(\mathbb{R}^N))$](gifs/ae.gif) .
.
See last page of this manuscript for details.
Show me the PDF file (275K), TEX file, and other files for this article.
 |
Hailiang Li Institute of Mathematics, University of Vienna A-1090 Vienna, Austria and Institute of Mathematics, Academia Sinica Beijing 100080, China email: hailiang.li@univie.ac.at |
|---|---|
 |
Chi-Kun Lin Department of Mathematics National Cheng Kung University Tainan 701, Taiwan email: cklin@math.cku.edu.tw |
Return to the EJDE web page