Electron. J. Diff. Eqns., Vol. 2003(2003), No. 86, pp. 1-8.
Estimates for derivatives of the Green functions for the noncoercive
differential operators on homogeneous manifolds of negative curvature, II
Roman Urban
Abstract:
We consider the Green functions for second order
non-coercive differential operators on homogeneous manifolds of
negative curvature, being a semi-direct product of a nilpotent Lie
group
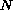 and
and
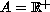 .
We obtain estimates for the mixed derivatives of the Green functions
that complements a previous work by the same author [17].
.
We obtain estimates for the mixed derivatives of the Green functions
that complements a previous work by the same author [17].
Submitted February 18, 2003. Published August 15, 2003.
Math Subject Classifications: 11E25, 43A85, 53C30, 31B25.
Key Words: Green function, homogeneous manifolds of negative curvature,
NA groups, evolutions on nilpotent Lie groups.
Show me the
PDF file (217K),
TEX file, and other files for this article.
 |
Roman Urban
Institute of Mathematics
University of Wroclaw
Pl. Grunwaldzki 2/4
50-384 Wroclaw, Poland
email: urban@math.uni.wroc.pl |
|---|
Return to the EJDE web page
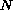 and
and
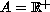 .
We obtain estimates for the mixed derivatives of the Green functions
that complements a previous work by the same author [17].
.
We obtain estimates for the mixed derivatives of the Green functions
that complements a previous work by the same author [17].
