Electron. J. Diff. Eqns., Vol. 2003(2003), No. 40, pp. 1-7.

Existence of solutions to higher-order discrete three-point problems

Douglas R. Anderson

Abstract:
We are concerned with the higher-order discrete three-point boundary-value problem
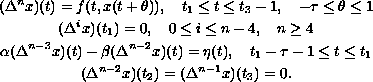
$$\displaylines{ (\Delta^n x)(t)=f(t,x(t+\theta)), \quad t_1\le t\le t_3-1, \quad -\tau\le \theta\le 1\cr (\Delta^i x)(t_1)=0, \quad 0\le i\le n-4, \quad n\ge 4 \cr \alpha (\Delta^{n-3}x)(t)-\beta (\Delta^{n-2}x)(t)=\eta(t), \quad t_1-\tau-1\le t\le t_1 \cr (\Delta^{n-2}x)(t_2)=(\Delta^{n-1}x)(t_3)=0. }$$
By placing certain restrictions on the nonlinearity and the distance between boundary points, we prove the existence of at least one solution of the boundary value problem by applying the Krasnoselskii fixed point theorem.

Submitted August 19, 2002. Published April 15, 2003.
Math Subject Classifications: 39A10.
Key Words: Difference equations, boundary-value problem, Green's function, fixed points, cone.

Show me the PDF file (177K), TEX file, and other files for this article.

Douglas R. Anderson
Department of Mathematics and Computer Science
Concordia College
Moorhead, MN 56562 USA}
email: andersod@cord.edu

Return to the EJDE web page