Electron. J. Diff. Eqns., Vol. 2003(2003), No. 12, pp. 1-21.
Oscillation for equations with positive and negative coefficients
and with distributed delay I: General results
Leonid Berezansky & Elena Braverman
Abstract:
We study a scalar delay differential equation with a bounded
distributed delay,
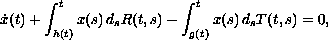
where
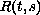 ,
,
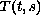 are nonnegative nondecreasing in
are nonnegative nondecreasing in
 for any
for any
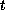 ,
,
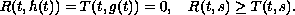
We establish a connection between
non-oscillation of this differential equation
and the corresponding differential inequalities,
and between positiveness of the fundamental
function and the existence of a nonnegative solution for a
nonlinear integral inequality that constructed explicitly.
We also present comparison theorems, and explicit
non-oscillation and oscillation results.
In a separate publication (part II), we will consider
applications of this theory to differential equations with several
concentrated delays, integrodifferential, and mixed equations.
Submitted October 29, 2002. Published February 11, 2003.
Math Subject Classifications: 34K11, 34K15.
Key Words: Oscillation, non-oscillation, distributed delay,
comparison theorems.
Show me the
PDF file (240K),
TEX file, and other files for this article.
A related article has been published by the same authors
in this journal:
Oscillation for equations with positive and negative coefficients
and with distributed delay II: Applications,
Vol. 2003(2003), No. 47, pp. 1-25.
 |
Leonid Berezansky
Department of Mathematics
Ben-Gurion University of the Negev
Beer-Sheva 84105, Israel
e-mail: brznsky@cs.bgu.ac.il |
|---|
 |
Elena Braverman
Department of Mathematics and Statistics
University of Calgary
2500 University Drive N. W.,
Calgary, Alberta, Canada, T2N 1N4
Fax: (403)-282-5150, phone: (403)-220-3956
email: maelena@math.ucalgary.ca |
|---|
Return to the EJDE web page
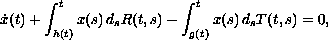
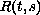 ,
,
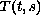 are nonnegative nondecreasing in
are nonnegative nondecreasing in
 for any
for any
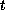 ,
,