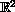
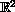
Imed Bachar, Habib Maagli, & Lamia Maatoug
Abstract:
We study the existence and the asymptotic behaviour of positive
solutions of the nonlinear equation
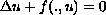 ,
in the domain
,
in the domain
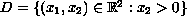 , with
, with
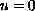 on
the boundary. The aim is to prove some existence results
for the above equation in a general setting by using a
fixed-point argument.
on
the boundary. The aim is to prove some existence results
for the above equation in a general setting by using a
fixed-point argument.
Submitted December 14, 2001. Published May 16, 2002.
Math Subject Classifications: 31A25, 31A35, 34B15, 34B27, 35J65.
Key Words: Singular elliptic equation, superharmonic function,
Green function, Schauder fixed point theorem, maximun principle.
Show me the PDF file (306K), TEX file, and other files for this article.
 |
Imed Bachar Departement de Mathematiques Faculte des Sciences de Tunis Campus universitaire 1060 Tunis, Tunisia e-mail: Imed.Bachar@ipeigb.rnu.tn |
|---|---|
 |
Habib Maagli Departement de Mathematiques Faculte des Sciences de Tunis Campus universitaire 1060 Tunis, Tunisia e-mail: habib.maagli@fst.rnu.tn |
 |
Lamia Maatoug Departement de Mathematiques Faculte des Sciences de Tunis Campus universitaire 1060 Tunis, Tunisia e-mail: Lamia.Maatoug@ipeit.rnu.tn |
Return to the EJDE web page