Electron. J. Diff. Eqns., Vol. 2001(2001), No. 54, pp. 1-18.
Asymptotic behaviour for Schrodinger equations with a quadratic
nonlinearity in one-space dimension
Nakao Hayashi & Pavel I. Naumkin
Abstract:
We consider the Cauchy problem for the Schr\"{o}dinger
equation with a quadratic nonlinearity in one space dimension
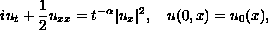
where
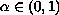 .
From the heuristic point of view,
solutions to this problem should have a quasilinear character when
.
From the heuristic point of view,
solutions to this problem should have a quasilinear character when
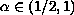 .
We show in this paper that the
solutions do not have a quasilinear character for all
.
We show in this paper that the
solutions do not have a quasilinear character for all
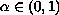 .
due to the special structure of the nonlinear term.
We also prove that for
.
due to the special structure of the nonlinear term.
We also prove that for
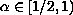 if the initial data
if the initial data
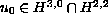 are small, then
the solution has a slow time decay such as
are small, then
the solution has a slow time decay such as
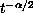 .
For
.
For
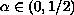 ,
if we assume that the initial data
,
if we assume that the initial data
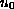 are
analytic and small, then the same time decay occurs.
are
analytic and small, then the same time decay occurs.
Submitted May 22, 2001. Published July 25, 2001.
Math Subject Classifications: 35Q55, 74G10, 74G25.
Key Words: Schrodinger equation, large time behaviour, quadratic nonlinearity.
Show me the
PDF file (302K),
TEX file, and other files for this article.
 |
Nakao Hayashi
Department of Mathematics
Graduate School of Science
Osaka University
Toyonaka, Osaka 560-0043, Japan
e-mail : nhayashi@math.wani.osaka-u.ac.jp
|
|---|
 |
Pavel I. Naumkin
Instituto de Fisica y Matematicas
Universidad Michoacana, AP 2-82
Morelia, CP 58040, Michoacan, Mexico
e-mail: pavelni@zeus.ccu.umich.mx |
|---|
Return to the EJDE web page
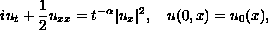
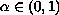 .
From the heuristic point of view,
solutions to this problem should have a quasilinear character when
.
From the heuristic point of view,
solutions to this problem should have a quasilinear character when
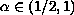 .
We show in this paper that the
solutions do not have a quasilinear character for all
.
We show in this paper that the
solutions do not have a quasilinear character for all
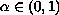 .
due to the special structure of the nonlinear term.
We also prove that for
.
due to the special structure of the nonlinear term.
We also prove that for
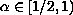 if the initial data
if the initial data
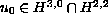 are small, then
the solution has a slow time decay such as
are small, then
the solution has a slow time decay such as
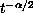 .
For
.
For
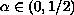 ,
if we assume that the initial data
,
if we assume that the initial data
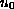 are
analytic and small, then the same time decay occurs.
are
analytic and small, then the same time decay occurs.

