Electron. J. Diff. Eqns., Vol. 2000(2000), No. 33, pp. 1-11.
Existence of solutions for a sublinear system of elliptic equations
Carlos Cid & Cecilia Yarur
Abstract:
We study the existence of non-trivial non-negative
solutions for the system
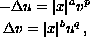
where p and q are positive constants with pq <1,
and the domain is the unit ball of
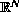 (N greater than 2) except for the center zero.
We look for pairs of functions that satisfy the above system and Dirichlet
boundary conditions set to zero. Our results also apply to some super-linear
systems.
(N greater than 2) except for the center zero.
We look for pairs of functions that satisfy the above system and Dirichlet
boundary conditions set to zero. Our results also apply to some super-linear
systems.
Submitted January 21, 2000. Published May 9, 2000.
Math Subject Classifications: 35A20, 35J60, 34B18.
Key Words: Semilinear elliptic systems, sub-harmonic functions,
super-harmonic functions
Show me the
PDF file (138K),
TEX file, and other files for this article.
Carlos Cid
Departamento de Ingenieria Matematica, Universidad de Chile
Casilla 170/3, Correo 3, Santiago, Chile
email: ccid@@dim.uchile.cl
Cecilia Yarur
Departamento de Matematicas, Universidad de Santiago de Chile
Casilla 307, Correo 2, Santiago, Chile
email: cyarur@@fermat.usach.cl
Return to the EJDE web page
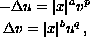
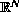 (N greater than 2) except for the center zero.
We look for pairs of functions that satisfy the above system and Dirichlet
boundary conditions set to zero. Our results also apply to some super-linear
systems.
(N greater than 2) except for the center zero.
We look for pairs of functions that satisfy the above system and Dirichlet
boundary conditions set to zero. Our results also apply to some super-linear
systems.