Electron. J. Diff. Eqns.,
Vol. 1997(1997), No. 16, pp 1-7.
Asymptotic instability of nonlinear differential equations
Rafael Avis & Raul Naulin
Abstract:
This article shows that the zero solution to the system
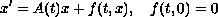
is unstable. To show instability, we impose conditions on the
nonlinear part
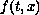 and on the fundamental matrix of the
linear system
and on the fundamental matrix of the
linear system
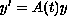 .
Our results generalize the instability results obtained by
J. M. Bownds, Hatvani-Pinter, and K. L. Chiou.
.
Our results generalize the instability results obtained by
J. M. Bownds, Hatvani-Pinter, and K. L. Chiou.
Submitted July 9, 1997. Published October 15, 1997.
Math Subject Classification:39A11, 39A10.
Key Words: Liapunov instability, h-stability.
Show me the
PDF file (141 KB),
TEX file, and other files for this article.
Rafael Avis & Raul Naulin
Departamento de Matematicas, Universidad de Oriente,
Cumana 6101 A-285. Venezuela
e-mail: rnaulin@cumana.sucre.udo.edu.ve
Return to the EJDE home page
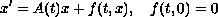
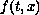 and on the fundamental matrix of the
linear system
and on the fundamental matrix of the
linear system
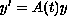 .
Our results generalize the instability results obtained by
J. M. Bownds, Hatvani-Pinter, and K. L. Chiou.
.
Our results generalize the instability results obtained by
J. M. Bownds, Hatvani-Pinter, and K. L. Chiou.