Electron. J. Differential Equations,
Vol. 2017 (2017), No. 55, pp. 1-7.
Global well-posedness for nonlinear nonlocal Cauchy problems
arising in elasticity
Hantaek Bae, Suleyman Ulusoy
Abstract:
In this article, we prove global well-posedness for a family of one
dimensional nonlinear nonlocal Cauchy problems arising in elasticity.
We consider the equation
![$$
u_{tt}-\delta Lu_{xx}=\big(\beta \ast [(1-\delta)u+u^{2n+1}]\big)_{xx}\,,
$$](gifs/aa.gif)
where
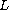 is a differential operator,
is a differential operator,
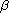 is an integral operator,
and
is an integral operator,
and
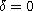 or 1. (Here, the case
or 1. (Here, the case
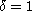 represents
the additional doubly dispersive effect.)
We prove the global well-posedness of the equation in energy spaces.
represents
the additional doubly dispersive effect.)
We prove the global well-posedness of the equation in energy spaces.
Submitted May 24, 2016. Published February 22, 2017.
Math Subject Classifications: 35Q74, 35L15, 74B20.
Key Words: Nonlinear nonlocal wave equations; kernel function; global solution.
Show me the PDF file (212 KB),
TEX file for this article.
 |
Hantaek Bae
Department of Mathematical Sciences
Ulsan National Institute of Science and Technology
(UNIST), Korea
email: hantaek@unist.ac.kr
|
|---|
 |
Süleyman Ulusoy
Department Of Mathematics and Natural Sciences
American University of Ras al Khaimah
PO Box 10021,Ras Al Khaimah, UAE
email: suleyman.ulusoy@aurak.ac.ae, suleymanulusoy@yahoo.com
|
|---|
Return to the EJDE web page
![$$
u_{tt}-\delta Lu_{xx}=\big(\beta \ast [(1-\delta)u+u^{2n+1}]\big)_{xx}\,,
$$](gifs/aa.gif)
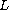 is a differential operator,
is a differential operator,
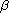 is an integral operator,
and
is an integral operator,
and
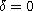 or 1. (Here, the case
or 1. (Here, the case
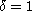 represents
the additional doubly dispersive effect.)
We prove the global well-posedness of the equation in energy spaces.
represents
the additional doubly dispersive effect.)
We prove the global well-posedness of the equation in energy spaces.

