Electron. J. Differential Equations, Vol. 2017 (2017), No. 304, pp. 1-24.

Non-homogeneous problem for fractional Laplacian involving critical Sobolev exponent

Kun Cheng, Li Wang

Abstract:
In this article, we study the existence of positive solutions for the nonhomogeneous fractional equation involving critical Sobolev exponent
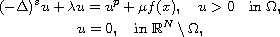
$$\displaylines{ (-\Delta)^{s} u +\lambda u=u^p+\mu f(x), \quad u>0\quad \text{in } \Omega,\cr u =0, \quad \text{in } \mathbb{R}^N\setminus \Omega, }$$
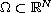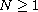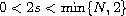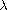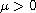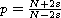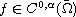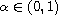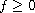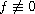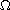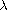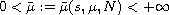where $\Omega\subset\mathbb{R}^N$ is a smooth bounded domain, $N\geq 1$, $0<2s<\min\{N,2\}$, $\lambda$ and $\mu>0$ are two parameters, $p=\frac{N+2s}{N-2s}$ and $f\in C^{0,\alpha}(\bar{\Omega})$, where $\alpha \in(0,1)$. $f\geq 0$ and $f\not \equiv 0$ in $\Omega$. For some $\lambda$ and N, by the barrier method and mountain pass lemma, we prove that there exists $0 <\bar{\mu}:= \bar{\mu}(s,\mu,N)< +\infty$ such that there are exactly two positive solutions if 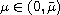$\mu \in (0,\bar{\mu})$ and no positive solutions for 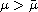$\mu>\bar{\mu}$. 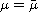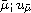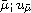Moreover, if $\mu=\bar{\mu}$, there is a unique solution ($\bar{\mu}; u_{\bar{\mu}}$), which means that ( $\bar{\mu}; u_{\bar{\mu}}$) is a turning point for the above problem. 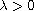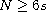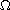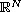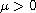Furthermore, in case $ \lambda > 0$ and $N \ge 6s$ if $\Omega$ is a ball in $\mathbb{R}^N$ and f satisfies some additional conditions, then a uniqueness existence result is obtained for $\mu>0$ small enough.

Submitted September 23, 2017. Published December 11, 2017.
Math Subject Classifications: 35A15,35J60, 46E35.
Key Words: Non-homogeneous; fractional Laplacian; critical Sobolev exponent; variational method.

Show me the PDF file (373 KB), TEX file for this article.

Kun Cheng
Department of Information Engineering
Jingdezhen Ceramic Institute
Jingdezhen 333403, China
email: chengkun0010@126.com
Li Wang
College of Science
East China Jiaotong University
Nanchang 330013, China
email: wangli.423@163.com

Return to the EJDE web page