Electron. J. Differential Equations,
Vol. 2016 (2016), No. 323, pp. 1-24.
Partial continuity for a class of elliptic systems with non-standard growth
Jihoon Ok
Abstract:
We study partial Holder continuity of weak solutions to elliptic systems
with variable non-standard growth, which are related to the function
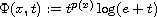 .
We prove that weak solutions are Holder
continuous for any Holder exponent, except Lebesgue measure zero sets,
if systems satisfy certain continuity assumptions.
In particular, the variable exponent functions p(.) are assumed to satisfy
so-called vanishing log-Holder continuity.
.
We prove that weak solutions are Holder
continuous for any Holder exponent, except Lebesgue measure zero sets,
if systems satisfy certain continuity assumptions.
In particular, the variable exponent functions p(.) are assumed to satisfy
so-called vanishing log-Holder continuity.
Submitted October 24, 2016. Published December 20, 2016.
Math Subject Classifications: 35B65, 35J60.
Key Words: Partial continuity; elliptic system; non-standard growth;
variable exponent.
Show me the PDF file (341 KB),
TEX file for this article.
Jihoon Ok
School of Mathematics
Korea Institute for Advanced Study
Seoul 02455, Korea
email: jihoonok@kias.re.kr
|
Return to the EJDE web page
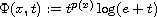 .
We prove that weak solutions are Holder
continuous for any Holder exponent, except Lebesgue measure zero sets,
if systems satisfy certain continuity assumptions.
In particular, the variable exponent functions p(.) are assumed to satisfy
so-called vanishing log-Holder continuity.
.
We prove that weak solutions are Holder
continuous for any Holder exponent, except Lebesgue measure zero sets,
if systems satisfy certain continuity assumptions.
In particular, the variable exponent functions p(.) are assumed to satisfy
so-called vanishing log-Holder continuity.