In this article we study the existence of solutions to the problem

where
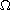 is a smooth bounded domain in
is a smooth bounded domain in

 and
and
 is a differentiable
function with g(x,0)=0 for all
is a differentiable
function with g(x,0)=0 for all
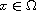 .
By using minimax methods
and Morse theory, we prove the existence of at least three nontrivial
solutions for the case in which an asymmetric condition on the nonlinearity
g is assumed. The first two nontrivial solutions are obtained by
employing a cutoff technique used by Chang et al in [9].
For the existence of the third nontrivial solution, first we compute the
critical group at infinity of the associated functional by using a technique
used by Liu and Shaoping in [19]. The final result is obtained by
using a standard argument involving the Morse relation.
.
By using minimax methods
and Morse theory, we prove the existence of at least three nontrivial
solutions for the case in which an asymmetric condition on the nonlinearity
g is assumed. The first two nontrivial solutions are obtained by
employing a cutoff technique used by Chang et al in [9].
For the existence of the third nontrivial solution, first we compute the
critical group at infinity of the associated functional by using a technique
used by Liu and Shaoping in [19]. The final result is obtained by
using a standard argument involving the Morse relation.

