We obtain the existence and multiplicity of positive
 -periodic solutions for the difference equations
-periodic solutions for the difference equations
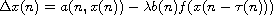
and
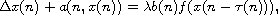
where
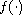 may be singular at
may be singular at
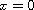 .
Using a fixed point theorem in cones, we extend recent results
in the literature.
.
Using a fixed point theorem in cones, we extend recent results
in the literature.
Yanqiong Lu
Abstract:
We obtain the existence and multiplicity of positive
 -periodic solutions for the difference equations
-periodic solutions for the difference equations
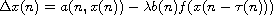
and
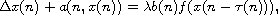
where
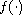 may be singular at
may be singular at
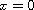 .
Using a fixed point theorem in cones, we extend recent results
in the literature.
.
Using a fixed point theorem in cones, we extend recent results
in the literature.
Submitted June 29, 2011. Published July 28, 2011.
Math Subject Classifications: 34G20.
Key Words: Positive periodic solutions; existence; nonexistence;
difference equations; fixed point.
Show me the PDF file (217 KB), TEX file, and other files for this article.
 |
Yanqiong Lu Department of Mathematics Northwest Normal University Lanzhou, 730070, China email: linmu8610@163.com |
|---|
Return to the EJDE web page