Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 153, pp. 1-9.
Existence of non-negative solutions for predator-prey elliptic
systems with a sign-changing nonlinearity
Jagmohan Tyagi
Abstract:
By the method of monotone iteration and Schauder fixed point theorem,
we prove the existence of non-negative solutions to the system
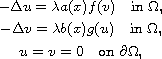
for
 sufficiently small, where
sufficiently small, where
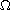 is a bounded
domain in
is a bounded
domain in
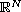 with smooth boundary
with smooth boundary
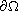 and
and
 is a positive parameter. In this work, we allow
the sign changing nature of a and b with
is a positive parameter. In this work, we allow
the sign changing nature of a and b with
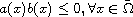 .
.
Submitted July 19, 2011. Published November 10, 2011.
Math Subject Classifications: 35J45, 35J55.
Key Words: Elliptic system; non-negative solution; existence.
Show me the PDF file (202 KB),
TEX file, and other files for this article.
 |
Jagmohan Tyagi
Indian Institute of Technology Gandhinagar
Vishwakarma Government Engineering College Complex
Chandkheda, Visat-Gandhinagar Highway, Ahmedabad
Gujarat, India - 382424
email: jtyagi1@gmail.com, jtyagi@iitgn.ac.in
|
|---|
Return to the EJDE web page
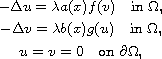
 sufficiently small, where
sufficiently small, where
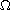 is a bounded
domain in
is a bounded
domain in
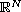 with smooth boundary
with smooth boundary
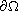 and
and
 is a positive parameter. In this work, we allow
the sign changing nature of a and b with
is a positive parameter. In this work, we allow
the sign changing nature of a and b with
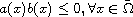 .
.
