Two nonlinear days in Urbino 2017.
Electron. J. Diff. Eqns., Conference 25 (2018), pp. 213-219.
Kirchhoff-type problems involving nonlinearities satisfying
only subcritical and superlinear conditions
Biagio Ricceri
Abstract:
In this note, we study the problem
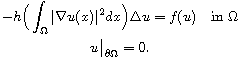
As an application of a general multiplicity result, we establish the
existence of at least three solutions, two of which are global minimizers
of the related energy functional. The only condition assumed on f
is that it be subcritical and superlinear;
no condition on the behaviour of f at 0 is required.
Published September 15, 2018.
Math Subject Classifications: 35J20, 35J61, 49K40, 90C26.
Key Words: Kirchhoff-type problems; multiplicity of global minimizers;
variational methods.
Show me the PDF file (206 K),
TEX and other files for this article.
Biagio Ricceri
Department of Mathematics
University of Catania
Viale A. Doria, 95125 Catania, Italy
email: ricceri@dmi.unict.it
|
Return to the table of contents
for this conference.
Return to the EJDE web page