In recent years a growing attention has been devoted to
-Laplacians, linear second-order degenerate elliptic
PDO's contained in the general class introduced by Franchi and Lanconelli
in some papers dated 1983--84 [12, 13, 14].
Here we present a survey on several results appeared in literature in
the previous decades, mainly regarding: (i) Geometric and functional analysis frameworks for the
's; (ii) regularity and pointwise estimates for the solutions to
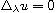;(iii) Liouville theorems for entire solutions;
(iv) Pohozaev identities for semilinear equations involving
-Laplacians; (v) Hardy inequalities;
(vi) global attractors for the parabolic and damped hyperbolic counterparts of the
's.
We also show several typical examples of
-Laplacians, stressing
that their class contains, as very particular examples, the celebrated
Baouendi-Grushin operators as well as the
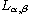and
operators respectively introduced by Thuy and Tri
in 2002 [36] and by Thuy and Tri in 2012 [37].
