Two nonlinear days in Urbino 2017.
Electron. J. Diff. Eqns., Conference 25 (2018), pp. 39-53.
Ground states of some coupled nonlocal fractional dispersive PDEs
Eduardo Colorado
Abstract:
We show the existence of ground state solutions to the following stationary
system coming from some coupled fractional dispersive equations such as:
nonlinear fractional Schrodinger (NLFS) equations (for dimension n=1,2,3)
or NLFS and fractional Korteweg-de Vries equations (for n=1),
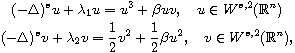
where
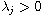 ,
j=1,2,
,
j=1,2,
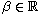 ,
n=1,2,3, and
n/4 < s < 1. Precisely, we prove the existence of a positive radially
symmetric ground state for any
,
n=1,2,3, and
n/4 < s < 1. Precisely, we prove the existence of a positive radially
symmetric ground state for any
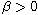 .
.
Published September 15, 2018.
Math Subject Classifications: 49J40, 35Q55, 35Q53, 35B38, 35J50.
Key Words: Nonlinear Fractional Schrodinger equation; variational method;
fractional Korteweg-de Vries equation; critical point theory;
ground state
Show me the PDF file (305 K),
TEX and other files for this article.
 |
Eduardo Colorado
Departamento de Matemáticas
Universidad Carlos III de Madrid
Avda. Universidad 30, 28911 Leganés
Madrid, Spain
email: eduardo.colorado@uc3m.es, eduardo.colorado@icmat.es
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
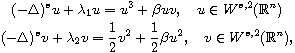
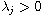 ,
j=1,2,
,
j=1,2,
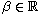 ,
n=1,2,3, and
n/4 < s < 1. Precisely, we prove the existence of a positive radially
symmetric ground state for any
,
n=1,2,3, and
n/4 < s < 1. Precisely, we prove the existence of a positive radially
symmetric ground state for any
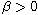 .
.
