International Conference on Applications of Mathematics to Nonlinear Sciences.
Electron. J. Diff. Eqns., Conference 24 (2017), pp. 47-61.
Differential equations of dynamical order
Andrei Ludu, Harihar Khanal
Abstract:
We introduce a special type of ordinary differential equations
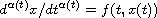
whose order of differentiation is a continuous function depending
on the independent variable t. We show that such dynamical order
of differentiation equations (DODE) can be solved as a Volterra
integral equations of second kind with singular integrable kernel.
We find the conditions for existence and uniqueness of solutions
of such DODE. We present the numeric approach and solutions for particular
cases for
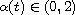 and discuss the asymptotic approach of
the DODE solutions towards the classical ODE solutions for
and discuss the asymptotic approach of
the DODE solutions towards the classical ODE solutions for
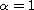 and 2.
and 2.
Published November 15, 2017.
Math Subject Classifications: 34A08, 45G10, 65D30.
Key Words: Dynamical order differential equation; fractional differential equation;
Voltera equationl; singular integrable kernel.
Show me the PDF file (600 K),
TEX file for this article.
 |
Andrei Ludu
Department of Mathematics
Embry-Riddle Aeronautical University
Daytona Beach, FL, USA
email: ludua@erau.edu
|
|---|
 |
Harihar Khanal
Department of Mathematics
Embry-Riddle Aeronautical University
Daytona Beach, FL, USA
email: harihar.khanal@erau.edu
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
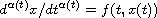
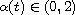 and discuss the asymptotic approach of
the DODE solutions towards the classical ODE solutions for
and discuss the asymptotic approach of
the DODE solutions towards the classical ODE solutions for
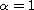 and 2.
and 2.

