International Conference on Applications of Mathematics to Nonlinear Sciences.
Electron. J. Diff. Eqns., Conference 24 (2017), pp. 11-22.
Global weak solutions to degenerate coupled diffusion-convection-dispersion
processes and heat transport in porous media
Michal Benes, Lukas Krupicka
Abstract:
In this contribution we prove the existence of weak solutions
to degenerate parabolic systems
arising from the coupled moisture movement,
transport of dissolved species and heat transfer
through partially saturated porous materials.
Physically motivated mixed Dirichlet-Neumann boundary conditions
and initial conditions are considered.
Existence of a global weak solution
of the problem is proved by means of semidiscretization in time
and by passing to the limit from discrete approximations.
Degeneration occurs in the nonlinear transport coefficients
which are not assumed to be bounded below and above by positive
constants. Degeneracies in all transport coefficients
are overcome by proving suitable a priori
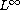 -estimates
for the approximations of primary unknowns of the system.
-estimates
for the approximations of primary unknowns of the system.
Published November 15, 2017.
Math Subject Classifications: 5A05, 35D05, 35B65, 35B45, 35B50, 35K15, 35K40
Key Words: Initial-boundary value problems for second-order parabolic systems;
global solution, smoothness and regularity of solutions;
coupled transport processes; porous media.
Show me the PDF file (251 K),
TEX file for this article.
 |
Michal Benes
Department of Mathematics
Faculty of Civil Engineering
Czech Technical University in Prague
Thakurova 7, 166 29 Prague 6, Czech Republic
email: michal.benes@cvut.cz
|
|---|
 |
Lukas Krupicka
Department of Mathematics
Faculty of Civil Engineering
Czech Technical University in Prague
Thakurova 7, 166 29 Prague 6, Czech Republic
email: lukas.krupicka@fsv.cvut.cz
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
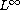 -estimates
for the approximations of primary unknowns of the system.
-estimates
for the approximations of primary unknowns of the system.

