In this article we consider a mathematical model of malaria transmission. We investigate both a reduced model which corresponds to the situation when the infected mosquito population equilibrates much faster than the human population and the full model. We prove that when the basic reproduction number is less than one, the disease-free equilibrium is the only equilibrium and it is locally asymptotically stable and if the reproduction number is greater than one, the disease-free equilibrium becomes unstable and an endemic equilibrium emerges and it is asymptotically stable. We also prove that, when the reproduction number is greater than one, there is a minimum wave speed
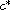such that a traveling wave solution exists only if the wave
speed c satisfies
.
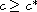Finally, we investigate the relationship
between spreading speed and diffusion coefficients. Our results show that
the movements of mosquito population and human population will speed up the
spread of the disease.
