2014 Madrid Conference on Applied Mathematics in honor of Alfonso Casal,
Electron. J. Diff. Eqns., Conference 22 (2015), pp. 47-51.
A convergence theorem for a two-species competition system with
slow diffusion
Georg Hetzer, Lourdes Tello
Abstract:
This article concerns the effect of slow diffusion in
two-species competition-diffusion problem with
spatially homogeneous nearly identical reaction terms.
In this case all (nonnegative) equilibria are spatially homogeneous,
and the set of nontrivial equilibria is the graph of a
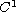 -curve.
This article shows convergence of positive solutions to an equilibria
which is determined by the initial data. The proof relies on the existence
of a Lyapunov function and is adapted from [6] which dealt with linear
diffusion.
-curve.
This article shows convergence of positive solutions to an equilibria
which is determined by the initial data. The proof relies on the existence
of a Lyapunov function and is adapted from [6] which dealt with linear
diffusion.
Published November 20, 2015.
Math Subject Classifications: 35K57, 35K65.
Key Words: Two-species competition-diffusion system; slow dispersal;
identical species; convergence to equilibria.
Show me the PDF(185 K),
TEX and other files for this article.
 |
Georg Hetzer
Department of Mathematics and Statistics
Auburn University
Auburn, AL 36849, USA
email: hetzege@auburn.edu
|
|---|
 |
Lourdes Tello
Department of Applied Mathematics
ETS Arquitectura, Universidad Politécnica de Madrid
28040 Madrid, Spain
email: l.tello@upm.es
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
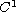 -curve.
This article shows convergence of positive solutions to an equilibria
which is determined by the initial data. The proof relies on the existence
of a Lyapunov function and is adapted from [6] which dealt with linear
diffusion.
-curve.
This article shows convergence of positive solutions to an equilibria
which is determined by the initial data. The proof relies on the existence
of a Lyapunov function and is adapted from [6] which dealt with linear
diffusion.

