2014 Madrid Conference on Applied Mathematics in honor of Alfonso Casal,
Electron. J. Diff. Eqns., Conference 22 (2015), pp. 19-30.
Existence and regularity of weak solutions for singular elliptic problems
Brahim Bougherara, Jacques Giacomoni, Jesus Hernandez
Abstract:
In this article we study the semilinear singular elliptic problem
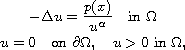
where
 is a regular bounded domain of
is a regular bounded domain of
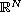 ,
,
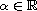 ,
,
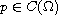 which behaves as
which behaves as
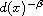 as
as
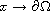 with
with
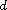 the distance function up to the boundary
and
the distance function up to the boundary
and
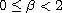 .
We discuss the existence, uniqueness and stability
of the weak solution. We also prove accurate estimates on the gradient
of the solution near the boundary. Consequently, we can prove that the
solution belongs to
.
We discuss the existence, uniqueness and stability
of the weak solution. We also prove accurate estimates on the gradient
of the solution near the boundary. Consequently, we can prove that the
solution belongs to
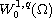 for
for
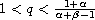 which is optimal if
which is optimal if
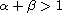 .
.
Published November 20, 2015.
Math Subject Classifications: 35B65.
Key Words: Semilinear elliptic and singular problems; comparison principle;
regularity of the gradient of solutions; Hardy inequalities.
Show me the PDF(265 K),
TEX and other files for this article.
 |
Brahim Bougherara
Département de mathématiques
ENS de Kouba
16308--Alger, Algérie
email: brahim.bougherara@univ-pau.fr
|
|---|
 |
Jacques Giacomoni
LMAP (UMR CNRS 5142) Bat. IPRA
Avenue de l'Université F-64013 Pau, France
email: jacques.giacomoni@univ-pau.fr
|
|---|
 |
Jesus Hernández
Departemento de Matemáticas
Universidad Autónoma de Madrid
28049 Madrid, Spain
email: jesus.hernandez@uam.es
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
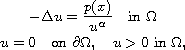
 is a regular bounded domain of
is a regular bounded domain of
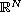 ,
,
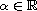 ,
,
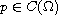 which behaves as
which behaves as
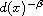 as
as
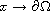 with
with
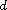 the distance function up to the boundary
and
the distance function up to the boundary
and
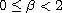 .
We discuss the existence, uniqueness and stability
of the weak solution. We also prove accurate estimates on the gradient
of the solution near the boundary. Consequently, we can prove that the
solution belongs to
.
We discuss the existence, uniqueness and stability
of the weak solution. We also prove accurate estimates on the gradient
of the solution near the boundary. Consequently, we can prove that the
solution belongs to
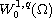 for
for
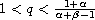 which is optimal if
which is optimal if
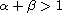 .
.


